他のことを調べていたら、中央攻撃のところで気になる箇所を見つけました。

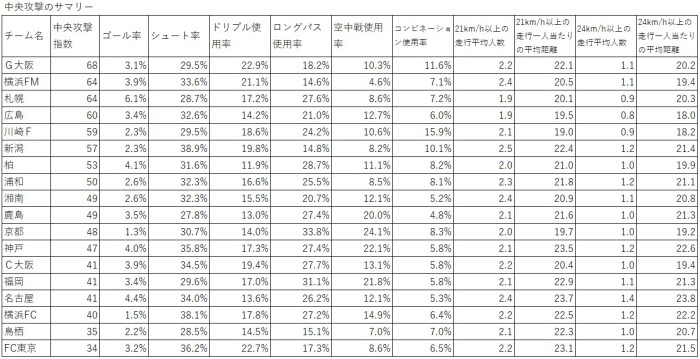
データは下記の中央攻撃サマリー（8/27（日）に公開されていたデータ）です。



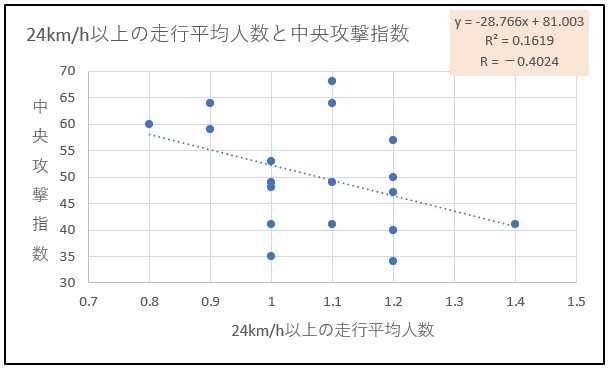
24km/h以上の走行平均人数と中央攻撃指数を散布図にしたところ、下記の通りになりました。

相関係数はギリギリ相関関係有りといってよい－0.4024でした。マイナスの符号がついている通り負の相関関係でした。24km/h以上の走行平均人数が増えるほど、中央攻撃指数が低くなる（中央攻撃回数が少なくなる）という関係です。


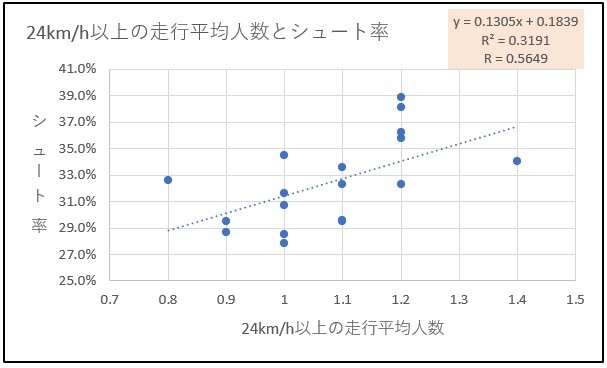
次は24km/h以上の走行平均人数とシュート率の関係です。

相関関係は0.5649で相関関係があります。符号がプラスのため、24km/h以上の走行平均人数が増えるほどシュート率が高くなるという関係です。


この二つを見ると矛盾しているように見えます。

この矛盾しているところが非常に気になりました。

指数とシュート率ではシュート本数は分かりません。もしかしたら24km/h以上の走行平均人数が多いほどシュート本数が多いのではないかとの仮説を立て、計算しました。


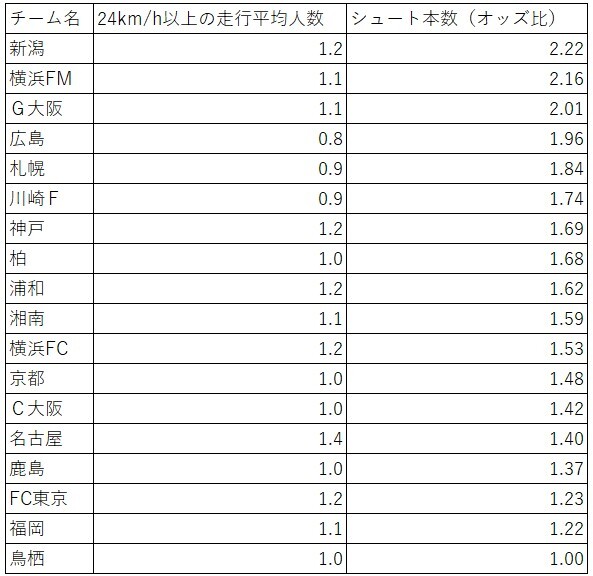
結果は下記の通りです。指数とシュート率からシュート本数を計算しました。

実際のシュート本数は計算できないため、オッズ比を計算しました。シュート本数が最も少ない鳥栖を1.00とすると、最も多いのが新潟で2.22となりました。鳥栖と新潟では2倍以上の差があるということです。

※オッズ比ってこれでよいのかどうかよく分かりませんが、意味は通じると思いますので、このまま続けます。


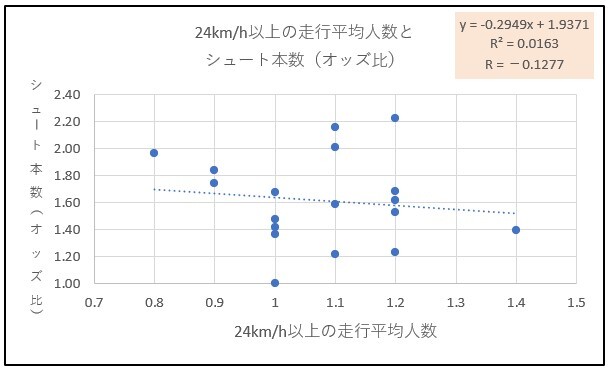
24km/h以上の走行平均人数とシュート本数（オッズ比）を下記の通り散布図にしました。

相関係数は－0.1277でほぼ無相関でした。24km/h以上の走行平均人数が多くなればなるほど、シュート本数が増えるのではないかと思いましたがそうではないようです。チームによって中央攻撃の仕方や、そもそも中央攻撃の志向度も異なるため、24km/h以上の走行平均人数という一つの軸で説明するのは無理があるようです。


結果が伴わないブログで申し訳ありませんが、以上で終わります。

いつものことながらFootball LABさんからデータを拝借しました。