先日「シュート位置の巻」シュート位置の巻 | SPORTERIAを投稿したところ、

『＞PA内にはGA内も含んでいますが、PA内よりもGA内の方が相関係数が低いことは意外でした。

確かに意外ですね！考えられる要因としては・GA内のシュートのほうが母数が少ない・PA内にはペナルティキック（PK）が含まれていて、GA内には含まれていないあたりでしょうか？ペナルティキックにはゴール期待値0.8ほど付くので、後者の方が影響は大きい気もします。』

とSPORTERIAスタッフ様からコメントをいただきました。ありがとうございます。せっかくですので、もう少し計算しました。


シュート位置ごとのゴール期待値データはなく、試合ごとのゴール期待値しかデータはありません。このことが、今回の計算結果に大きく影響しそうです。ゴール期待値が目的変数、シュート位置が説明変数、みたいな感じになりますかね。


「ペナルティキックにはゴール期待値0.8ほど付く」とのことです。正確なゴール期待値は分かりませんので、PKシュート1本ごとに、シュート1本とゴール期待値を0.8減らし再集計しました。その後相関係数を求めました。

結果は気の通りです。

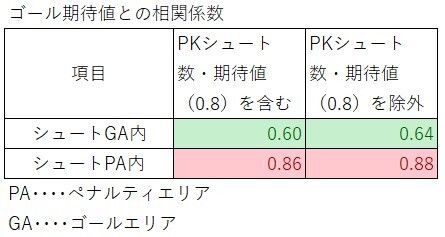
左側の数値が元の数値（相関係数）、右側が今回再集計した後の数値（相関係数）です。

結果はシュートPA内の方がシュートGA内よりも相関が強かったです。


次は相関係数ではなく、単純な平均シュート数を集計しました。


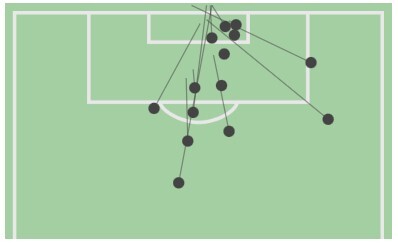
この平均シュート数は、

このような図をもとに、目で判断し集計した結果です。目視による集計ですので誤差を含んでいます。J-STATSのシュート数とは若干異なりますがご容赦ください。

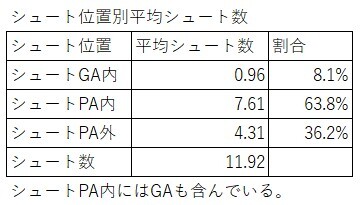
GA内平均シュート数は1試合当たり0.96本、PA内は7.61本です。％にすると全体シュート数の63.8%がPA内、8.1％がGAです。

圧倒的にPA内の方が多いです。GA内は１試合に1本あるかないかくらいの出現度です。


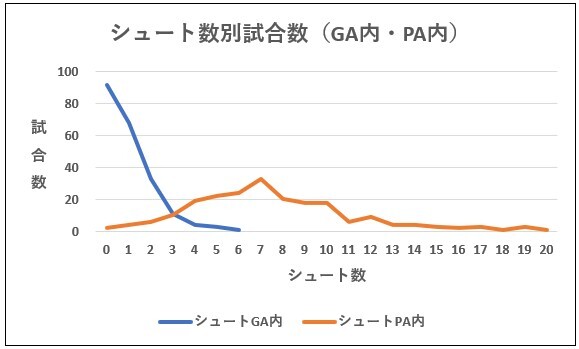
シュート数別試合数をGA内、PA内ごとに可視化したのが下図です。

歴然とした差があります。GA内はポアソン分布様です。多くの試合でシュートGA内は0本であり、PA内と比べると、GA内でシュートが発生するのは”まれ”であることが分かります。

PA内は正規分布様です。ちなみにPA内のグラフの尖度と歪度を計算すると（Excelが計算してくれます）、下表の通りでした。

尖度、歪度ともに絶対値で1未満でした。「双方とも絶対値で1未満の場合、実務的には正規分布とみなす」と教わった記憶がありますので、PA内シュート数は正規分布といって良いのでしょう。またPA内の平均シュート数は7.61本ですので、GA内よりも影響度が強いと思われます。



以上を総合的に見ると、シュートGA内はPA内よりも非常に少なく、仮にシュート1本当たりのゴール期待値が高くても全体（試合ごとのゴール期待値）に及ぼす影響は少ないと思われる。よってシュートGA内よりもシュートPA内の方が相関係数が高くなるのではないかと思います。



毎度のことながらFootball LABさんからデータを拝借しました。